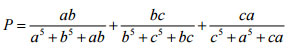Đề thi vào lớp 10 môn Toán sở GD&ĐT Hải Dương
Đề thi vào lớp 10 môn Toán sở GD&ĐT Hải Dương – Đề thi tuyển sinh vào lớp 10 THPT môn Toán sở GD&ĐT Hải Dương năm 2016 – 2017 được Đề Thi Thử sưu tầm và đăng tải nhằm giúp các em học sinh có thêm nhiều tài liệu ôn thi vào lớp 10 môn Toán để tham khảo chuẩn bị tốt cho kì thi tuyển sinh sắp tới đây đạt kết quả cao. Mời các em cùng tham khảo.
Đề thi vào lớp 10 môn Toán sở GD&ĐT Hải Dương
Câu 1 (2,0 điểm) Giải phương trình và hệ phương trình sau:
a) (x + 3)2 = 16
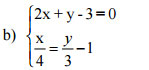
Câu 2 (2,0 điểm)
a) Rút gọn biểu thức: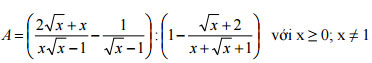 
b) Tìm mđể phương trình: x2 – 5x + m – 3 =0 có hai nghiệm phân biệt x1, x2 thỏa mãn x12 – 2x1x2 + 3×2 =1
Câu 3 (2,0 điểm)
a) Tìm a và b biết đồ thị hàm số y = ax + b đi qua điểm A(-1; 5) và song song với đường thẳng y = 3x + 1
b) Một đội xe phải chuyên chở 36 tấn hàng. Trước khi làm việc, đội xe đó được bổ sung thêm 3 xe nữa nên mỗi xe chở ít hơn 1 tấn so với dự định. Hỏi đội xe lúc đầu có bao nhiêu xe? Biết rằng số hàng trở trên tất cả các xe có khối lượng bằng nhau.
Câu 4 (3,0 điểm) Cho nửa đường tròn (O) đường kính AB. Gọi C là điểm cố định buộc đoạn thẳng OB (C khác 0 và B). Dựng đường thẳng d vuông góc với AB tại điểm C, cắt nửa đường tròn (0) tại điểm M. Trên cung nhỏ MB lấy điểm N bất kỳ (N khác M và B), tia AN cắt đường thẳng d tại điểm F, tia BN cắt đường thẳng d tại điểm E. Đường thẳng AE cắt nửa đường tròn (O) tại điểm D (D khác A)
a) Chứng minh: AD.AE = AC.AB.
b) Chứng minh: Ba điểm B, F, D thẳng hàng và F là tâm đường tròn nội tiếp tam giác CDN.
c) Gọi I là tâm đường tròn ngoại tiếp tam giác AEF. Chứng minh rằng điểm I luôn nằm trên một đường thẳng cố định khi điểm N di chuyển trên cung nhỏ MB.
Câu 5 (1,0 điểm) Cho a, b, c là ba só thực dương thỏa mãn: abc = 1
Tìm giá trị lớn nhất của biểu thức 
